A function specifies a systematic relation between one set and another set. To define a function f from set \mathcal{X} to set \mathcal{Y} , we write f: \mathcal{X} \to \mathcal{Y}
– \mathcal{X} is in this case called the domain of the function (the set where it takes input values).
– \mathcal{Y} is called the co-domain/range of the function (the set where it takes output values).
– Both \mathcal{X} and \mathcal{Y} can either be discrete or continuous sets.
Example
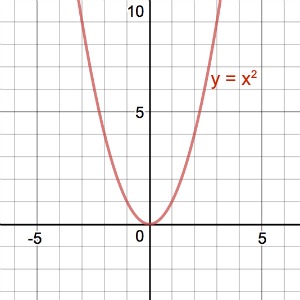
y = f(x) = x^2 maps every value in domain \mathcal{X} \in \mathbb{R} to range \mathcal{Y} \in \mathbb{R}^+ (since a squared number is always positive).